CoMaL - CoMaL: Good Features to Match on Object Boundaries

Swarna K Ravindran and Anurag Mittal

Indian Institute of Technology Madras

                 CVPR 2016 PDF                          CODE                         Additional Results                              Download CoMaL dataset [1] [2] [3]



Abstract

Traditional Feature Detectors and Trackers use information aggregation in 2D patches to detect and match discriminative patches. However, this information does not remain the same at object boundaries when there is object motion against a significantly varying background. In this paper, we propose a new approach for feature detection, tracking and re-detection that gives significantly improved results at the object boundaries. We utilize level lines or iso-intensity curves that often remain stable and can be reliably detected even at the object boundaries, which they often trace. Stable portions of long level lines are detected and points of high curvature are detected on such curves for corner detection. Further, this level line is used to separate the portions belonging to the two objects, which is then used for robust matching of such points. While such CoMaL (Corners on Maximally-stable Level Line Segments) points were found to be much more reliable at the object boundary regions, they perform comparably at the interior regions as well. This is illustrated in exhaustive experiments on real-world datasets.



We define our corners on level lines, which are lines connecting points having the same intensity. Portions on these level lines that do not move much when the intensity is varied are portions with good perpendicular gradients on the level line and are called stable in this work. When additionally, such level lines turn, then such corner points can be discriminated from other points in the neighborhood and detected as feature points.

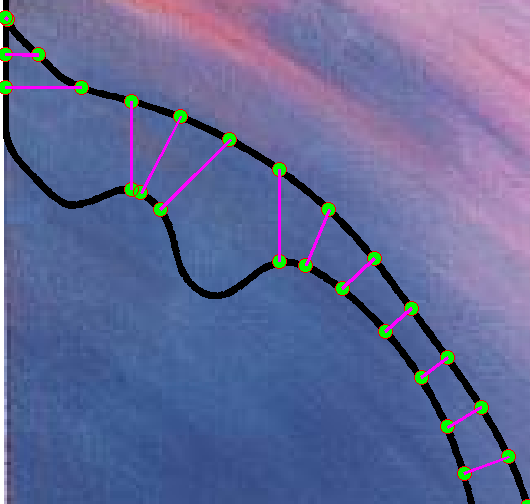
The stability of a level line is defined by computing the distance between neighboring level lines (Figure 3).

Figure 3. Stable and Unstable level lines in brown (top right) and blue (bottom right) boxes respectively. The Green level line is tested by considering the neighboring level lines in red and purple respectively. Note that the lines are very close in the brown box due to which they mostly overlap in the illustration.

The distance between neighboring level lines may be calculated using a variety of measures, one of which is to compute the euclidean distance between corresponding points. The problem associated with this is shown in Figure 4(a). We use an area based measure to overcome this, and make it more robust by computing Gaussian weighted areas (Figure 4(b)). The advantage in this is shown in Figure 5.

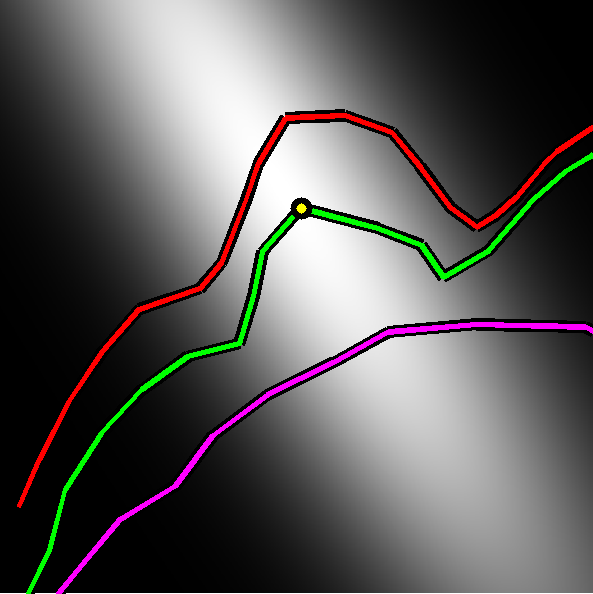Figure 4. (a) Problems with computing correspondences on neighbouring curves at concave and convex points. An area based measure is more robust.
 (b) Gaussian weighting centered on the yellow candidate corner on a level line.
Figure 5. Shows two level lines in red with their neighboring level lines in white. The Gaussian weighting at the point p (green) helps identify the level line in (a) as unstable and the one in (b) as stable.

Given the stability of the level line segments, a non-maximal suppression is finally done by picking only those segments that have a higher stability value than their immediate neighbors. Such maximally stable level line segments are denoted as MLL in this work.

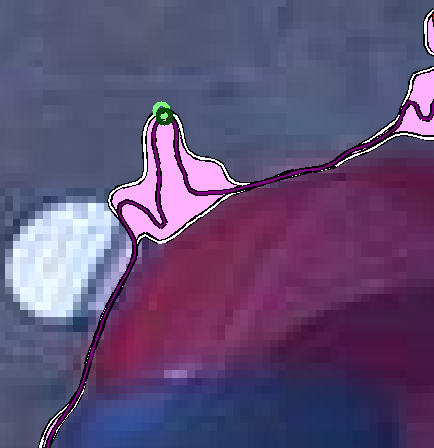
The corners on MLLs are distinctive and can be differentiated from other points in the neighborhood. The distribution of points on the curve centered at the candidate corner point p is determined (Figure 6) using their second moment (covariance) matrix. The eigenvalues of this matrix reflect the distribution of the points along two principal orthogonal directions and high values of both indicate a corner [3].

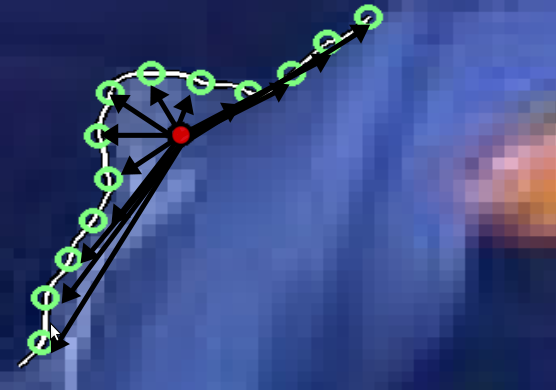Figure 6. The vectors connecting the points (in green) on the level line segment to their mean point. The distribution of these vectors is used to determine the cornerness of this level line segment.

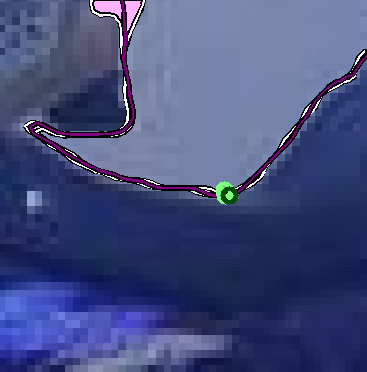
A point p is a feature point at scale s if it is maximally stable according to the stability measure and the cornerness of p is the local maxima along the level line at scale s. The entire algorithm is shown in Figure 7.

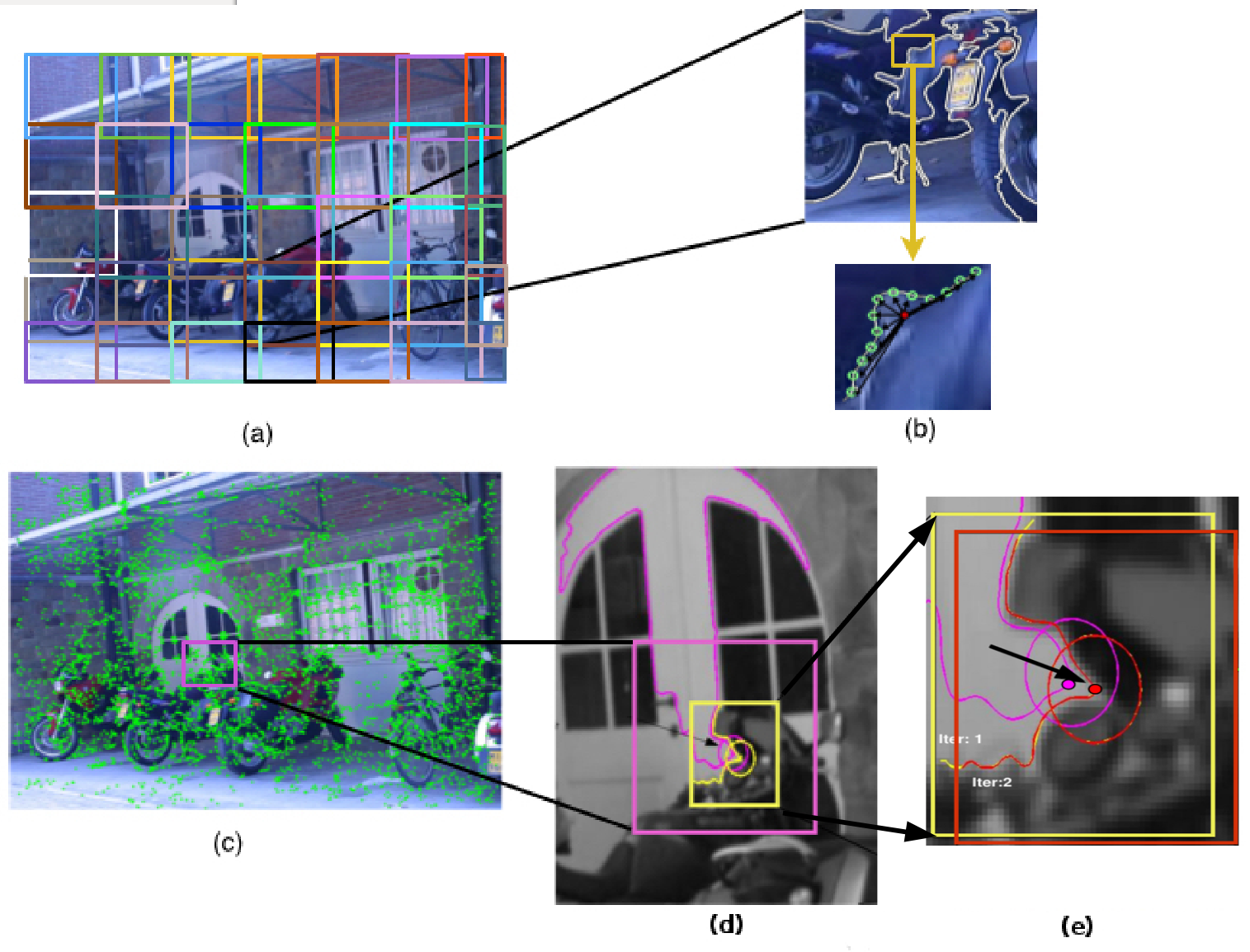Figure 7. An Image divided into overlapping blocks of size 2Bs. Different blocks are shown in different colors for clarity purposes. (b) A sample MLL in one sample block (top) and a corner found on it (bottom). (c) The set of initial corners detected. (d \& e) The iterative procedure for point refinement. The MLL and the initial point (pink) detected in the initial stage with a block window of size 2Bs are used to center a block (yellow) of size Bs in the first step of the iteration. This point moves to the red point. When the window is now centered at this (red) point, it remains the same and is thus detected as the final corner.


Matching

We use the level line associated with a point to separate the object from the background at the boundary and match the two patches separately using a Sum of Squared Differences (SSD) approach as shown in Figure 8 and 9.

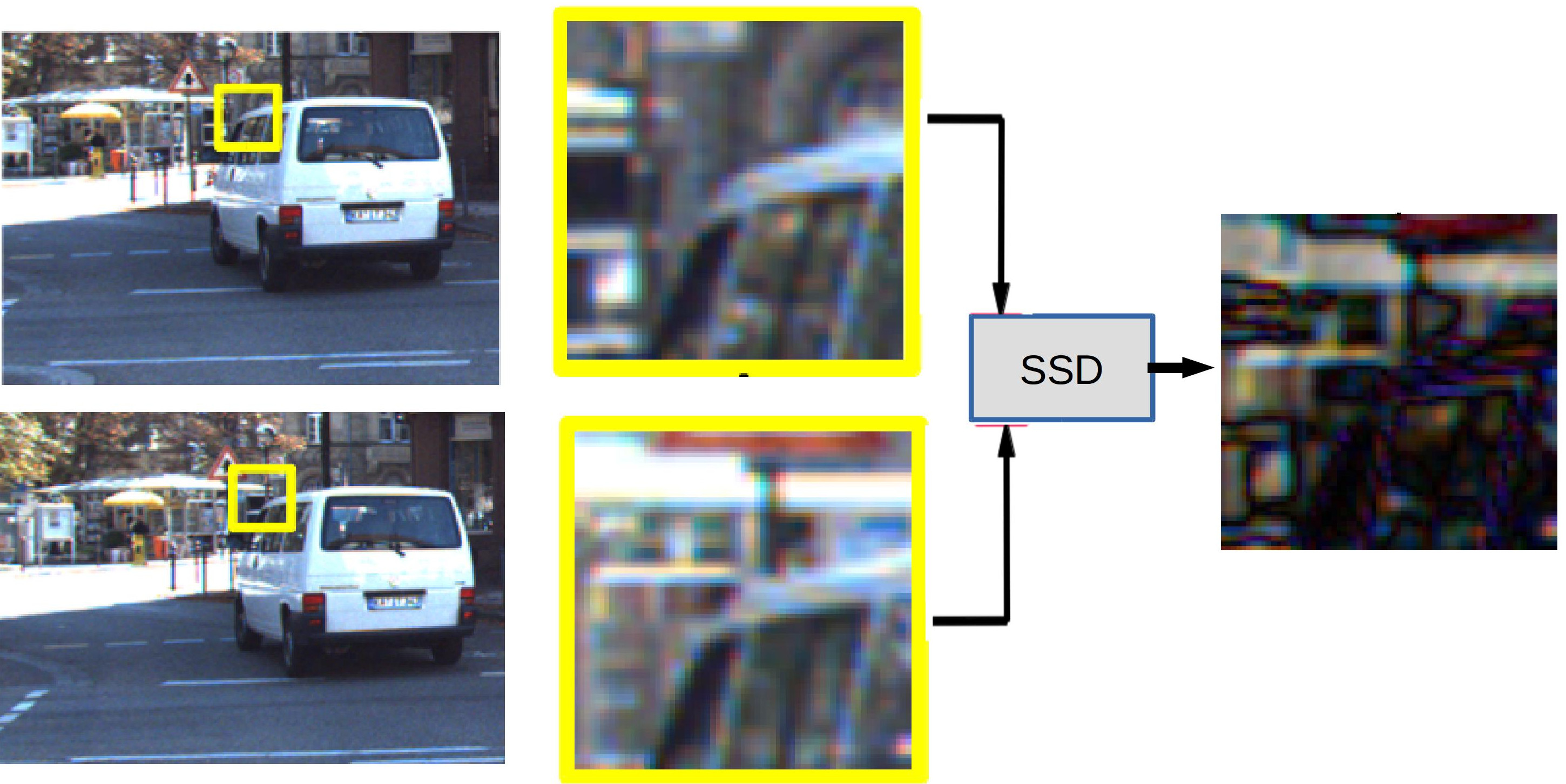Figure 8. The yellow boxes show feature patches in two frames where the object has moved to a different location. The difference image obtained by taking SSD between the two full patches (without a level line based separation) is shown in the last column where we can see that high values (brighter) correspond to locations from the background where the patch is substantially different. Low values (darker) on the difference image correspond to object portions whose intensity values are very similar.


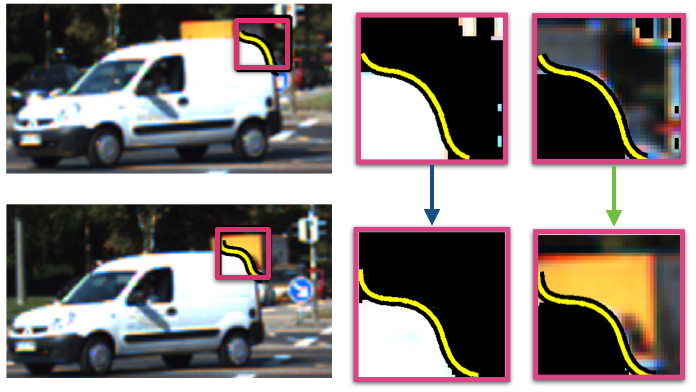Figure 9. Level line based matching. (a) +ve region (side with higher intensities) and (b) -ve region (side with lower intensities) separated by the level line shown in yellow. They are matched separately for better matching.




References

[1] G. Zhang, and Z. Dong, J. Jia et al. Efficient non-consecutive feature tracking for structure-from-motion. In ECCV 2010.

[2] J. Matas, O. Chum, M. Urban, and T. Pajdla. Robust wide baseline stereo from maximally stable extremal regions. In BMVC, 2002.

[3] C. Harris and M. Stephens. A combined corner and edge detector. In Alvey vision conference, 1988.

[4] A. Geiger, P. Lenz, C. Stiller, and R. Urtasun. Vision meets robotics: The KITTI dataset. In The International Journal of Robotics Research, 2013.

[5] K. Mikolajczyk and C. Schmid. Scale & affine invariant interest point detectors. In IJCV, 2004.

[6] D. Lowe. Distinctive Image Features from Scale-Invariant Keypoints. In IJCV 2004.

[7] E. Rosten and T. Drummond. Machine learning for high-speed corner detection. In ECCV 2006.

[8] J. Byrne and J. Shi. Nested shape descriptors. In ICCV 2013.

[9] B. Lucas, T Kanade et al. An iterative image registration technique with an application to stereo vision. In IJCAI 1981.